3.1.3 Eulers equation

Eulers equation

Eulers equation is used in pumps to describe fluid dynamics for ideal incompressible fluids with constant density. Figure 3.8 shows a pump impeller with associated velocity vector diagrams. Fluid flow enters the impeller at a velocity c₁ at a radius r₁. The fluid leaves the impeller at a radius r₂ with a velocity c₂. The design of the blade forces the relative velocity, i.e. the velocity which is experienced by an observer travelling with the movement of the blade, to alter its size and direction from w₁ to w₂. Due to this the absolute velocity c₂ at the impeller outlet will also deviate from the flow velocity c₁ at entry. The tangential component of absolute velocity is designated by c_u, i.e. in the direction of the peripheral speed

1 Installation — Figure 3.13a Impeller with velocity vector diagrams at inlet and outlet. (pumpportal.com)

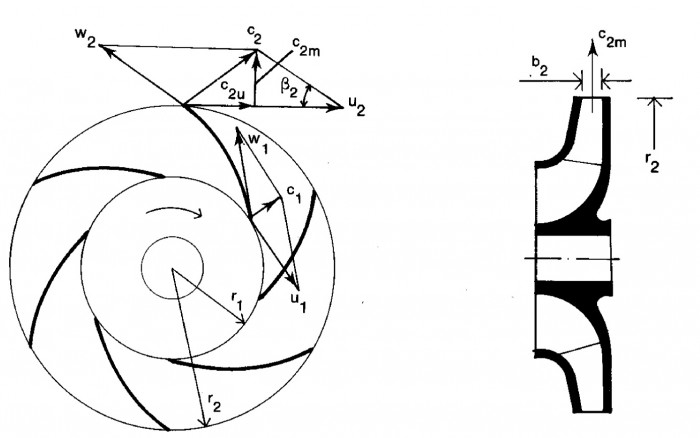
By applying the known law of momentum from fluid mechanics to the flow through the impeller, we obtain in the tangential direction the following equation:

Equ 3.8

Here M_t, is the rotary moment (torque), with which the impeller must affect the fluid, in order that the flow according to figure 3.8 may be obtained. The flow velocities in equation 3.8 are intended to be representative mean values for the medium which is flowing through the impeller. During the time Δt the pump shaft rotates through the angle Δφ at the same time as the mass Δm passes in and an equally large mass Δm passes out through the impeller.

If both lines are multiplied by Δφ and at the same time ṁ = Δm/Δt is introduced, then

Equ. 3.9

but M_t * Δφ/Δm is the work per unit of mass which the rotary moment carries out whilst the impeller rotates through angle Δφ

This work per unit of mass is called blade work and is designated I_b. Furthermore, the quotient Δφ/Δt is equal to the constant angular velocity ω of the pump impeller. Thus

Equ. 3.10

That part of the blade work which corresponds to the blade losses results in an increase of the internal energy of the medium whilst the rest ( h · I_b) provides a useful alternation of the state of the liquid (g • H). If then the peripheral speed u = r · ω is applied, we finally obtain

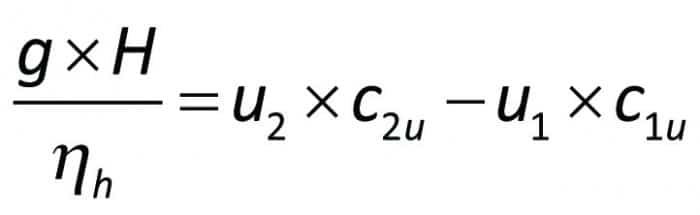
Equation 3.11 is Eulers equation as it is normally written for pumps, where:

g = acceleration due to gravity 9,806 (m/s²)
H = Head (m)
η_h = hydraulic efficiency
u = peripheral velocity (m/s)
c_u= tangential component of the absolute velocity (m/s)