8.3 Momentum equation
Momentum equation
The product of mass times flow velocity for a liquid particle is called its momentum. The momentum equation for steady flow reads:
The resultant F of all external forces on a control volume is equal to the changes in momentum for the outflowing and inflowing mass per unit time, or,
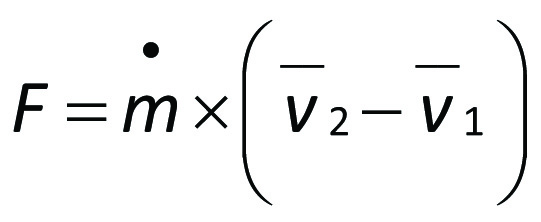
where
F = force (N)
ṁ = mass flow Δm/Δt (kg/s)
v = velocity vector (m/s)
The momentum equation is illustrated in the following example. The problem is to determine the force F required to hold a pipe bend in position.
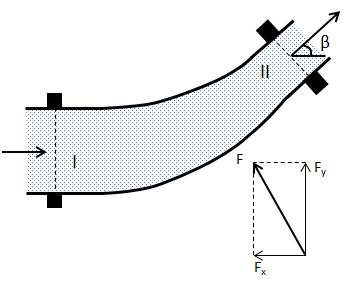
The control volume is considered to include the (exterior of the pipe) bend precisely. Then, for the arbitrary bend in the x axis:
For a 90° bend ß = 90°, therefore:
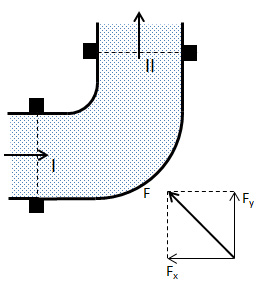
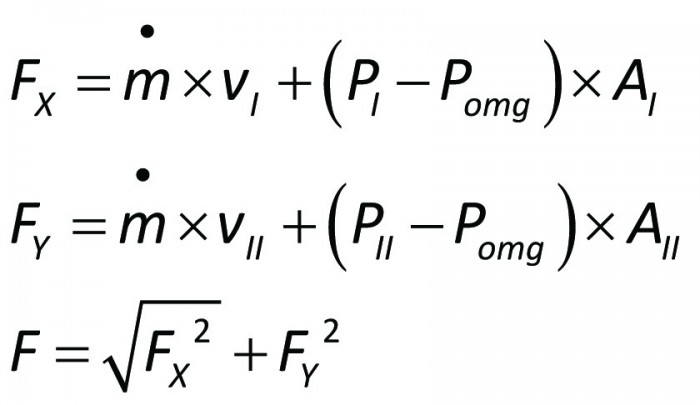
Note that it is a gauge pressure and not the absolute pressure in the pipe which determines the magnitude of the force. Note also that the forces can be determined without detailed knowledge of the internal flow process through the bend. The momentum equation applies regard-less of whether the process has losses or not.
lt is often the case that the terms ṁ and v are small compared with the others. For a 90° bend with AI being equal to AII
F = √2 * (p – pamb) * A
where
p = absolut pressure in the pipe (Pa)
pamb = ambient pressure (Pa)
A = cross sectional area of the pipe (m²)
F = fixing force (N)
The fixing force has an angle of 135° to the incoming direction of flow.

