7 Properties of liquids

Properties of liquids for pumping

All necessary information about properties of liquids for the purposes of pumping. Thorough explanations of the meanings of the terms in which various parameters of liquids are defined, explained and set out in examples. The most common liquids, water, oils and certain suspensions, are treated in greater depth than other liquids in separate sections.

Introduction and explanation of terms

Liquids, together with solids and gases, are the forms in which substances occur in nature. We speak of the solid state, the liquid state and the gaseous state. A solid body subjected to a very small shear force undergoes, independent of its plastic characteristics, only an elastic deformation.

A fluid when subjected to an arbitrarily small shear force undergoes a continuous deformation. This happens regardless of the sluggishness of the fluid. For a fluid the magnitude of the shear force and the speed of deformation are directly related. In a solid body it is the deformation itself which is related to the shear force.

A fluid may be either a liquid or a gas. A liquid differs from a gas in that, contrary to the gas, it is almost in-compressible. A gas, the condition (i .e. pressure and temperature) of which is such that the gas is close to the limit of conversion to a liquid, is usually called a vapor.

A substance can exist in all three states. A typical example of this is ice, water and steam. When ice is heated at constant pressure, the ice converts to water at the melting point and to steam at the boiling point; if the steam pressure is increased at constant temperature, the steam converts to water at the saturation (vapor) pressure.

Solid particles can be suspended in pure liquid. Such a liquid, pure liquid plus particles, is called a suspension. When the particles distribute themselves evenly through the liquid, we speak of a condition of homogeneous flow. When concentration gradients occur, we speak of a heterogeneous condition.

The word solution refers to an otherwise pure liquid in which a solid, liquid or gaseous substance has been dissolved.

Two liquids which are not soluble in each other, can be mixed by mechanical action. Such a mixture is called an emulsion.

Liquids generally display greatly varying properties. For the purposes of pumping the following characteristics of liquids should generally be known:

• viscosity
• melting point
• boiling point
• vapor pressure
• density, volumetric expansion
• compressibility, speed of wave propagation
• pH value
• fire hazard class, risk to health and environment.
• temperature

Viscosity

Viscosity (ability to flow, sluggishness) is a property of liquids treated under the heading of rheology. The word rheology derives from the Greek ” rheos” meaning flow. Between two layers of liquid flowing at different speeds, a tangential resistance, a shear stress, is developed because of molecular effects. We say that the shear stress is caused by the internal friction of the liquid, or conversely that the liquid transmits shear forces by reason of its internal friction.

A liquid in motion is continuously deformed by the effects of the shear forces. The magnitude of the stress depends on the rate of shear deformation and the sluggishness of the liquid, i.e. the viscosity.

Viscosity is defined for flow in layers, laminar flow, by Newton’s Law of viscosity.

 

 

 

 

 

 

 

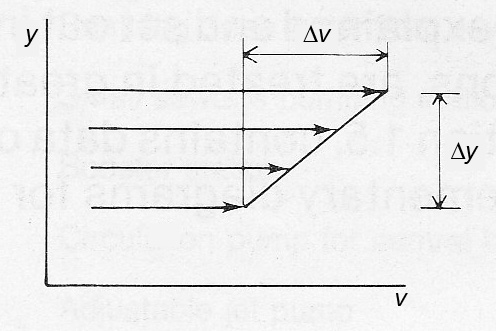
Figure 7a Definition of viscosity

Newton’s Law of viscosity
τ = μ (Δv / Δy)      (Equ. 7a)

τ = shear stress (N/m²)
μ = dynamic viscosity (Pa s)
Δv = change in velocity (m/s)
Δy = distance between layers (m)

The dynamic viscosity is stated in the Sl system as the unit

1 Pa s which is equivalent to 1Ns/m² or 1 kg m‾¹ s‾¹

Dynamic viscosity is sometimes called Absolute viscosity and other commonly used units for dynamic viscosity are:

1 Poise = 0.001 Pa s (the unit Poise is named after Jean Léonard Marie Poiseuille) or more often refereed to as 1 centipoise (1 cP) = 1 Pa s

In viscous flow equations the dynamic viscosity is divided by the density of the liquid, given the symbol v (Greek letter nu), this parameter is called kinematic viscosity.

ν = μ / ρ     (Equ. 7b)

where

ν = kinematic viscosity (m²/s)

μ = dynamic viscosity (Pa s)

ρ = density (kg/m³)

The SI unit for kinematic viscosity is 1 m²/s.

Sometimes, for convenience, the following units are used:

1 Stoke (1St) = 10‾⁴ m²/s
or more usually
1 cSt = 10‾² St = 10‾⁶ m²/s = 1 mm²/s

For the unit 1 cSt = 1 mm²/s, the kinematic viscosity of water at 20°C and 0.1 MPa (1 bar) has the numerical value of 1.

Newtonian liquids

A liquid which follows Newton’s Law of viscosity in laminar flow and has constant viscosity, regardless of shear rate and time, is known as a Newtonian liquid.

 

 

 

 

 

 

 

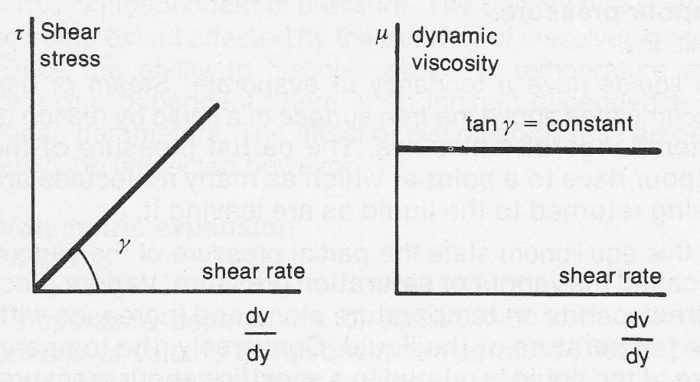
Figure 7b Newtonian liquid

Examples of Newtonian liquids are: Water, aqueous solutions, low molecular liquids, oils and oil distillates. Black liquor, liquid resin and resinous sebacic acid also behave like Newtonian liquids.

Non-Newtonian liquids

Liquids which do not fulfill the requirements for Newtonian liquids are called non-Newtonian liquids. Most high molecular liquids, suspensions and emulsions display non-Newtonian properties. Non-Newtonian liquids usually fall into three main groups:

1. Non-time-dependent liquids
   pseudo-plastic
   dilatant
   plastic
2. Time dependent liquids
   thixotropic
   rheopectic
   irreversible
3. Visco-elastic liquids

Non-time-dependent liquids

Non-time-dependent liquids (Group 1) are not effected by the length of time of the process of flow. The shear stress in the case of laminar flow at a given temperature is determined entirely by the shear rate. In analogy with Newtonian liquids, we may say:

τ = μ¹ (Δv / Δy)      (Equ. 7c)

where μ¹ = apparent (equivalent) dynamic viscosity.

 

 

 

 

 

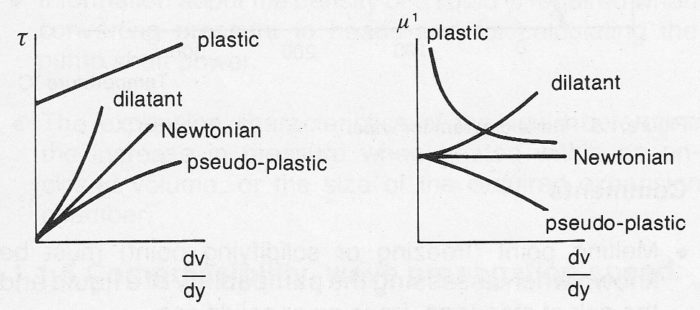
Figure 7c Non-time-dependent non-Newtonian liquids.

In the case of pseudo-plastic liquids, the apparent viscosity decreases with increasing shear rate.

Examples:
High molecular solutions, rubber, latex, certain molten materials, mayonnaise.

In the case of dilatant liquids the apparent viscosity increases with increasing shear rate.

Examples:
Base in oil paints, suspensions with high concentrations of small particles: cement, lime, sand, starch.

Plastic liquids require a certain minimum shear stress, yield stress, in order to initiate flow. The apparent viscosity decreases from an infinitely high value as the shear rate increases.

Examples:
Toothpaste, ointments, grease, margarine, paper pulp, printers ink, emulsions.

Time dependent liquids

In Time dependent liquids (Group 2), the apparent viscosity is affected not only by the shear rate but also by the length of time during which the flow continues.

 

 

 

 

 

 

 

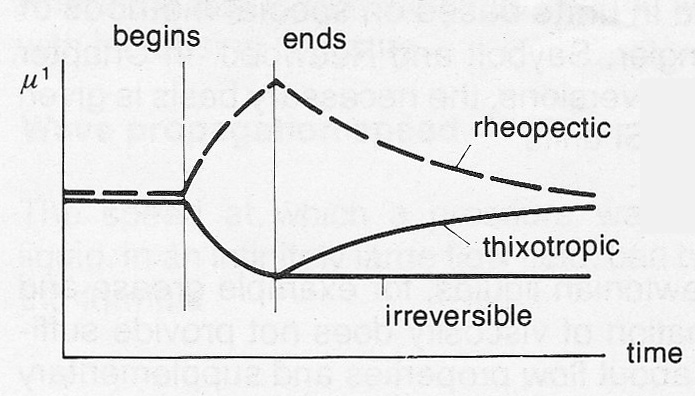
Figure 7d Illustrations of time-dependent non-Newtonian liquids.

The curves illustrated in figure 7d apply for constant values of shear rate and temperature.

In the case of thixotropic liquids, μ¹ diminishes when flow commences. When the flow ceases, the liquid returns to its original viscosity after a certain period of time.

Examples:
Paint, geletised foodstuffs.

Rheopectic liquids display increasing viscosity under mechanical influence and resume their original viscosity when the influence ceases.

Examples:
Certain suspensions of gypsum

Irreversible liquids do not resume their original viscosity at all or perhaps only after a very long time after the removal of the influence.These liquids have to be pumped carefully.

Examples:
Cheese coagulates, yoghurt, marmalade.

Visco-elastic liquids

Visco-elastic liquids (Group 3), contains liquids exhibiting both elastic and viscous properties. Visco-elastic liquids undergo both elastic and viscous deformations. When the flow ceases there is a certain reversal of elastic deformation.

Examples:
Asphalt, liquid nylon, rubber, polymer solutions.

Comments on liquid viscosity

• Dynamic viscosity is temperature-dependent. Increasing temperature results in diminishing viscosity. Certain liquids have to be heated for pumping.
• Temperature dependence of density has also to be considered in kinematic viscosity. At very high pressure > 10 MPa a certain pressure dependence can be observed in the viscosity.
• Loss coefficients in pipe flows are dependent upon Reynold’s number which is in turn dependent upon dynamic viscosity.
• The performance of centrifugal pump depends upon Reynold´s number. Pump data is always stated for water and this has to be corrected when pumping other liquids. High viscosity liquids are best pumped by positive displacement pumps.
• Viscosity is defined as the ratio of shear stress and shear rate in laminar flow. In the case of turbulent flow, this ratio is affected by exchange of momentum between the layers caused by the superposed random motion of the liquid particles.
• According to the older system of measurement, viscosity was stated in units based on special methods of testing, e.g. Engler, Saybolt and Redwood.

Liquid viscosity penetration test

For some non-Newtonian liquids, for example grease and asphalt, determination of viscosity does not provide sufficient information about flow properties and supplementary information regarding consistency is required. This information is obtained from determination of penetration. For greases, penetration is a measure of consistency. That is the depth, in tenths of a millimetre, to which a cone forces its way down into a test receptacle containing a grease sample heated to 25°C. The penetration depends on whether the consistency is changed by stirring, shaking and so on. Hard greases have low penetration figures whilst soft greases have high penetration. Manufacturers of greases state the penetration figure for each quality, e.g. 240-325. Two lubricant greases, furthermore, may have the same penetration figure but may still have different flow capabilities depending upon the viscosity of their respective component oils.

Determination of penetration for asphalt is carried out at 25°C in the same way, in principle, as with lubricant grease, but using a loaded pin instead of a cone. The values measured are used to classify asphalt, typical penetration figures being 10-50.

Melting point

The melting point is the temperature, here we use the unit °C (after the Swedish scientist Anders Celsius), at which a material changes from a solid to a liquid state. The melting point coincides with the temperature at which a liquid changes from a fluid to a solid state, the freezing or solidifying temperature.

The melting point in most substances is pressure-dependent only to a very limited degree. In those cases where the pressure dependence has to be taken into account, the boundary between solid and liquid state is shown by the melting curve in a pressure-temperature diagram.

Boiling point

The boiling point is the temperature at which a liquid converts to steam or gas at a particular local pressure. The boiling point is usually stated at 101.3 kPa (760 mm Hg). The boiling point of water at this pressure is 100°C. The boiling point of all liquids is heavily dependent upon pressure.

Vapor pressure (Unit, Pa)

All liquids have a tendency to evaporate. Steam or gas accumulates above the free surface of a liquid by reason of interchange of molecules. The partial pressure of the vapor rises to a point at which as many molecules are being returned to the liquid as are leaving it.

At this equilibrium state the partial pressure of the vapor is called the vapor or saturation pressure. Vapor pressure depends on temperature alone and increases with the temperature of the liquid. Conversely, the temperature of the liquid is related to a specific vapor pressure.

At a particular temperature, the equilibrium pressure above the surface of a liquid can never be less than the vapor pressure. Any attempt to lower the pressure of the vapor (by means of a vacuum pump for example) immediately results in increased evaporation, i.e. the liquid boils.

If the pressure in a liquid decreases locally to the vapor pressure at the actual temperature, vapor bubbles are generated in the liquid. In a pump installation, the formation of vapor bubbles (Cavitation) can cause serious mechanical damage and can seriously diminish the performance of the installation.

Various liquids display widely differing values of vapor pressure as a function of temperature. A material in a solid state can also change directly to the gaseous state without passing through the liquid state. As an example, a complete pressure-temperature diagram, showing the phases for water is illustrated below. At the triple point, all three states may exist simultaneously.

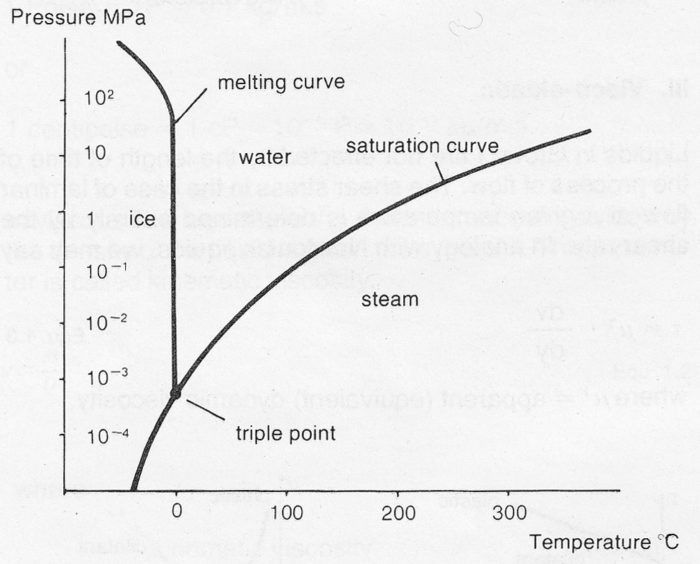
Figure 7e Phase diagram for water

Comments on liquid temperature and pressure for pumping

• Melting point (freezing or solidifying point) must be known when assessing the pumpability of a liquid and the risk of stoppage, freezing or solidifying.
• information regarding the vapor pressure is required for calculating the permitted suction lift, for choice of type of pump and shaft seal, and for assessment of risk of cavitation in the pump or pump system.

Density

Unit kg/m³, symbol ρ (roh)

The density of a liquid (also known as specific gravity or SG) is the relationship between the mass of the liquid and its volume. The density of liquids changes with temperature but is virtually  independent of pressure, the word in-compressible is some times used to describe this. The density of a liquid is to some extent affected by the quantity of dissolved gases. Since the ability to dissolve gases is temperature and pressure dependent, there is an indirect dependence on these parameters. The effect of dissolved gases can generally be neglected however.

Volumetric expansion

Unit 1/°C
Temperature dependence of density has to do with the change of volume of liquid with temperature. The expansion of a liquid due to a change of temperature can computed by the use of the expansion coefficient.

ΔV = V * ϒ * Δt      (Equ. 7d)

where

ΔV = change of volume (m³)
V = original volume (m³)
ϒ = coefficient of expansion (1/°C)
Δt = temperature change (°C)

Alternatively, the volume of a liquid due to a change in temperature can be determined by the densities.

V₂ = V₁ (ρ¹ / ρ²)      (Equ. 7e)

where

V₁ = volume at temperature t₁
V₂ = volume at temperature t₂
ρ¹ = density at temperature t₁
ρ² = density at temperature t₂

As a rule, the volume of a liquid increases with temperature.

Comments

• Information about the density of a liquid is required when converting pressure to heads and for calculating the pump shaft power (pump shaft power is sometimes refereed to as break power or break horse power).
• The expansion characteristics of the liquid determine the increase in pressure when heated within an enclosed volume, or the size of the required expansion chamber.

Compressibility

All liquids are compressible to an extent. This compressibility can generally be neglected. In certain aspects, however, compressibility is of decisive significance. Such situations are propagation of pressure waves in liquids and compression of enclosed volumes of liquid. It may be noted for example that water is about 100 times more elastic than steel. Compressibility is expressed in terms of the bulk modulus defined by the relationship:

K = ρ (Δ_P / Δρ) = -V (Δ_P / ΔV)      (Equ. 7f)

where

K = bulk modulus of the liquid (N/m²)
Δ_P = change of pressure (Pa)
Δρ = change of density (kg/m³)
V = volume of liquid (m³)
ΔV = change of volume of liquid (m³)

The change in volume due to a change in pressure can be calculated directly from the definition

ΔV = – ((V * Δ_P) / K))      (Equ. 7g)

where the minus sign indicates that the volume decreases with increasing pressure

Wave propagation speed

The speed at which a pressure wave propagates in a liquid, in an infinitely large flow field, can be calculated from the formula

a = √ (K / ρ)      (Equ. 7h)

where

a = wave propagation speed (m/s)
K = bulk modulus for the liquid (N/m²)
ρ = density of the liquid (kg/m³)

In a pump installation the effect of the elasticity of the pipe walls must also be considered. The wave propagation speed of a pressure wave in a pipe is:

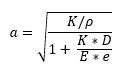
where

D = the diameter of the pipe (m)

E = elastic modulus of pipe material (N/m²)

e =  thickness of pipe walls (m)

The wave propagation speed is very sensitive to the presence of undissolved gas bubbles in the liquid.

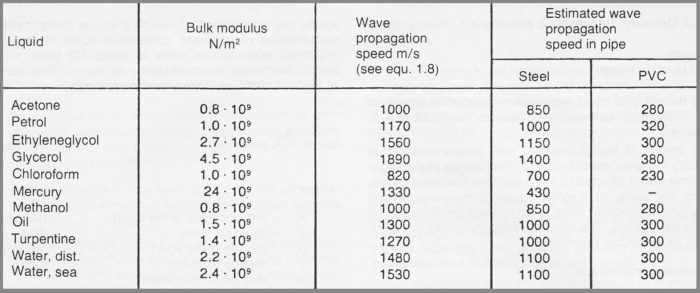
Figure 7f Elastic properties of some liquids at 25°C and 0.1 MPa (1 bar)

pH value

The concentration of hydrogen ions in an aqueous solution is a measure of the acidity of the solution and is expressed as the pH value.
The definition of the pH value is:

pH = – ¹⁰log H⁺

where H⁺ = the concentration of hydrogen ions (mol/l)

If, for example, H⁺ = 10^-4 mol/l, then the pH value = 4.

The hydrogen exponent is another name for the pH value.

The numerical value of pH varies between the limits 0-14. Acid solutions have pH values between 0 and 6.5, neutral solutions pH = 6.5-7.5 and the alkaline or base solutions pH = 7.5-14. Acid solutions turn blue litmus red and alkaline solutions turn red litmus blue.

All aqueous solutions reacting as acids contain a surfeit of hydrogen ions H⁺. All aqueous solutions reacting as alkalis have a surfeit of hydroxide ions OH ^–. The product of the hydrogen ion concentration and the hydroxide ion concentration is always a constant at any fixed temperature.

At 22°C for example the ion product is:

H⁺ * OH ^– = 10^-14 mol/l

When the hydrogen ion concentration and the hydroxide ion concentration are equal, i.e.

H⁺ OH ^– = 10^-7 then

pH = 7 and the solution reacts neutrally.

Pure water is a very poor electrical conductor. Water only acquires good conductivity in solutions of so-called electrolytes such as salts, acids or bases. When dissolved in water, these substances split into two components with opposing electrical charges, by means of which an electric current may be carried. This act of splitting is called electrolytic dissociation. The charged particles so formed are called ions. Distinction is made between the positively charged cation particles and the negatively charged anion particles. The positively charged particles are symbolized by + and the negatively charged particles by – . Metals and hydrogen in acids produce cations by electrolytic dissociation. The acid remnants and the alkaline hydroxyl groups on  the other hand generate negatively-charged anions.

For liquids with pH values of less than 4, the hydrogen ion concentration is a powerful factor affecting the speed of the dissolving process for most metals. The positively-charged hydrogen ions relinquish their charge at the surface of the metal to the metal atoms and break down their solid connections, whilst they themselves, robbed of their ion construction, return to the atomic state and unite into molecules leaving the metal surface in the form of gas bubbles. The dissolving process is faster, therefore, when the concentration of hydrogen ions is greater, i.e. the lower the pH value of the liquid.

Within the pH range of about 4 to 9, the oxygen present in the liquid, from air for example, has an influence on the corrosion process, say, for iron. The discharged hydrogen does not leave in the form of gas bubbles, as is the case with pH values in the region of 0 to 4, but combines immediately with the oxygen to produce water. At the same time the iron is oxidized to rust.

Figure 7g Illustration of pH values. The materials quoted can be regarded as a first introduction to the choice of materials in relation to Properties of liquids. See also section about Materials for pumps