10.3 Storage volumes for on-off control
Storage volumes for on-off control
Storage volumes for on-off control and pump sump volumes, see figure 10.3a, are most easily calculated by the use of a filling time, time constant, for the various partial volumes V1 and V2, and so on, defined as:

Time t1 thus corresponds to the time taken to fill volume V1 with flow Q1.
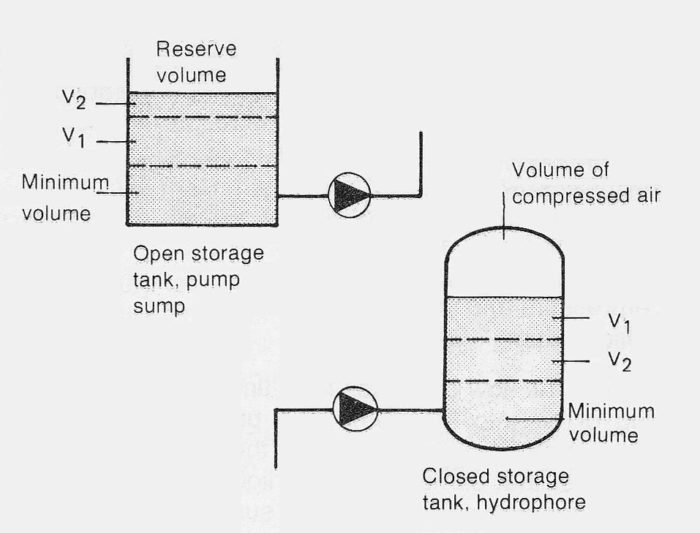
Figure 10.3a Storage with associated minimum volumes, partial volumes V1 and V2 and the volume of air for various arrangements.
In the case of a hydrophore, Q varies because of counter pressure from the pre-compressed volume of air, so that it is the mean value of this which should be used. Time t1 for the pump switched in first depends exclusively on the number of permitted starts per unit time, depending on whether starting is applied to several pumps alternately.

where
m = number of starts per hour per pump if the pumps are not alternated
and
m = number of starts per hour for the whole installation, if the pumps are alternated.
Here the number of starts per hour is a maximum when the mean flow per hour is equal to half the maximum flow. The times t2 , t3 , t4 , etc, are heavily dependent upon the operational Sequences A, B and C. Table 10.3a. shows various values for up to 4 pumps connected in parallel. In the table it is assumed that no more pumps are included in each operational sequence range than are needed to satisfy the flow requirements, see also the example which follows.
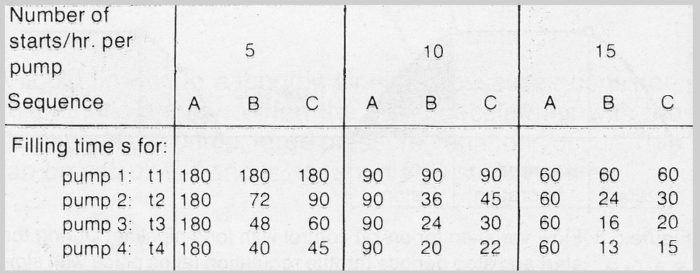
Table 10.2a. Table for determination of filling time for partial volumes in storage/pump sumps. The values are approximate for Sequence B, since there is a certain dependence on the flow increment from the various pumps
The air volume in a hydrophore is calculated using Boyle’s law, i.e. the isothermic relationships are assumed to apply, figure 10.3b.
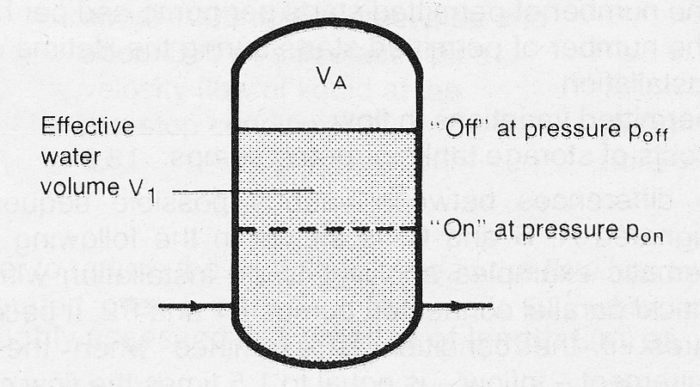
Figure 10.3b Hydrophore with designations for volume determination
At the absolute pressures poff and pon there are respectively the volumes of air VAoff and VAon:
poff * VAoff = pon * VAon = pi* VAi (Equ. 10.3c)
where
pi = absolute pressure at initial consitions i.e
pa = atmospheric pressure if the hydrophore is not pre-compressed
p = precompression pressure if the hydrophore is precompressed
VAi = initial volume of air
Using the effective volume of water V1 = VAon * VAoff we get:
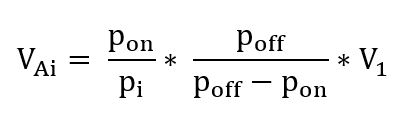
Combining equations 10.3a and 10.3b, if only one pump of volume flow Q1 delivers to the hydrophore, we then get:

where
V1 = Total volume of hydrophore if it is not precompressed (m³)
VAi = Volume of air in the hydrophore when precompressed. The total volume is usually chosen about 30% greater (m³)
pon = Absolute switch-on pressure determined by the system curve at volume flow Q1 (kPa)
poff = Absolute switch-off pressure (kPa)
pi = Absolute initial pressure atmospheric pressure without compression or precompression, pressure referred to volume VAi (kPa)
Q1 = Volume flow from pump, being the mean value of flow at pon and poff (m³/s)
m = maximum number of starts per hour per pump (n/h)
If several pumps are working on the same hydrophore, the effective water volumes V1, V2, V3 etc. are determined for each one as above. The various on and off switching pressures are then bound entirely by Boyle’s Law, Equ. 10.3c, which necessitates a careful quantifying of the various quantities.
