8.8 Total head loss in pipe system
Total head loss in pipe system
Total head loss in pipe system consist of the sum of the straight pipe head losses and the head losses in fittings, valves and other components.
hL = hLp (straight pipe) + hLfv ( fittings and valves) (Equ. 8.8a)
With the usual symbols
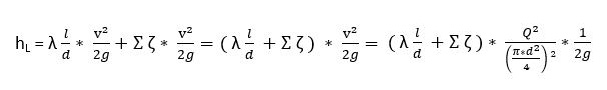
hL = head loss (m)
λ = loss coefficient for straight pipe (also known as Darcys friction factor)
ζ = loss coefficient for fittings, valves etc.
Σζ = sum of all loss coefficients
l = length of pipe (m)
d = diameter of pipe (m)
Q = volume flow (m³/s)
v = flow velocity (m/s)
For a given pipe system (l, d) the loss coefficients ζ and λ are independent of Q for a fully developed turbulent flow (large Re) in rough pipe.
The head loss can then be expressed as
hL= constant * Q²
The head loss, i.e. the pressure drop due to friction measured in metres column of liquid, increases as the square of the flow rate through the pipe. If the flow rate doubles the head loss increases by a factor of four.

Figure 8.8a Variations of head loss with flow rate in rough piping and at fully turbulent flow.
Note that Equation 2.26a does not apply to laminar flow or for turbulent flow in hydraulically smooth piping. With laminar flow and for a given pipe system both the straight pipe losses and the losses in fittings vary with Reynolds number. By expressing the losses in fittings in terms of equivalent pipe lengths, we get:
hL = constant * λ * leq * Q²
= constant * 64/Re* Q²
= constant * Q
Thus, in the case of laminar flow, the head loss varies proportionally with the flow rate.

Figure 8.8b Change of head loss with flow rate in laminar flow.
Comments
The treatment of pipe flow losses in Section 2.2 applies to Newtonian liquids of which the commonest is water. The non-Newtonian liquids require special attention regarding the determination of pressure losses. A special type of flow loss is caused by control valves in the pipe system. The control valve pressure losses are dealt with from a sizing point of view in section Valve pressure drop >>>
